Lors d’un entretien d’embauche, le géant Google pose des questions complexes mais basées sur la réflexion et la logique. Cela le distingue des autres recruteurs douteux dont les questions sont sensiblement plus bizarres, stupides ou trop personnelles…
Les quelques exemples de questions posées par Google sont intéressants.
Je me suis amusé à tenter de répondre ici à ces questions :
-
- 1. Combien de balles de golf peuvent tenir dans un bus scolaire ?
On divise le volume intérieur du bus par le volume standard d’une balle de golf. Il faut au moins 1,5 million de balles de golf.
-
- 3. Combien devriez-vous payer pour laver toutes les vitres de Seattle ?
Je ne paye rien. Je ne peux pas payer les quelques millions de dollars pour faire laver les vitres de Seattle (un peu plus de 100 000 maisons et bâtiments).
-
- 5. Expliquez le terme « base de données », en trois phrases, à votre neveu de 8 ans.
Première réponse possible : je n’ai rien à expliquer car je n’ai pas de neveu.
Deuxième réponse : cela dépend du QI du neveu… 😉 Une base de données sert à conserver de nombreuses informations ; cela est utile pour des institutions comme les banques et les assurances qui doivent gérer les informations sur leurs clients ; le moteur Google diffuse les résultats des requêtes à partir de sa base de données, car les informations sur les sites web sont conservées dans une base de données lorsqu’un référencement a été effectué.
Troisième réponse : Google est ton ami… (sous-entendu : démerde toi toi-même). 😉
-
- 6. Combien de fois par jour les aiguilles d’une horloge se chevauchent-elles ?
Les aiguilles se chevauchent à ces heures précises : 00:00, 01:05, 02:10, 03:15, 04:20, 05:25, 06:30, 07:35, 08:40, 09:45, 10:50, 11:55, 12:00, 13:05, 14:10, 15:15, 16:20, 17:25, 18:30, 19:35, 20:40, 21:45, 22:50, 23:55, minuit. Soit 25 fois. Mais en apparence, car en réalité la petite aiguille avance quand la grande aiguille avance. Par exemple, en réalité, à 15:15 ou à 03:15, les aiguilles ne se chevauchent pas, elles forment un angle de 7,5°, car la petite aiguille est bien sur 3 mais seulement quand il est 3 heures pile. Quand il est 03:15, la petite aiguille a avancé d’un angle de 7,5°. Il y a chevauchement quand il est un peu plus de 03:15, et plus précisément à 03:16:21. Ce décalage implique que les deux aiguilles se chevauchent 22 fois par jour, et non 25 fois.
Je pose :
360 n + 0,5 t = 6 t
Sachant que la grande aiguille avance de 6° par minute, et la petite aiguille de 0,5° par minute, l’égalité ci-dessus où n est un entier compris entre 0 et 24 permet de déterminer les valeurs de t.
Le chevauchement de l’aiguille des minutes et celle des heures a lieu toutes les 65,4545 minutes, soit toutes les 1h05min27,27s.
Par conséquent : 1440 minutes (soient 24h) divisées par 65,4545 = 22 (en arrondi). Les deux aiguilles se chevauchent 22 fois en 24 heures.
-
- 7. Vous devez aller d’un point A à un point B. Vous ne savez pas si vous pouvez y arriver. Que feriez-vous ?
Ne rien faire est le meilleur moyen d’échouer. Il faut agir quand même, on avisera après. On peut échouer, certes, mais on n’a cependant pas la certitude de ne pas réussir. Citation pertinente du célèbre écrivain Mark Twain : « Ils ne savaient pas que c’était impossible alors ils l’ont fait ». Ce sont souvent surtout nos craintes qui nous poussent à l’inaction, pas la besogne elle-même.
« L’audace réussit à ceux qui savent profiter des occasions » (Marcel Proust)
-
- 8. Imaginez que vous avez une armoire pleine de chemises et qu’il vous est très difficile d’en trouver une. Comment optimiser votre rangement pour retrouver vos chemises plus facilement ?
C’est paradoxal de ne pas trouver de chemise dans une armoire pleine de chemises… Non ?
Un truc simple : toutes les chemises sont identiques, la même couleur, ainsi on ne s’embarrasse pas de choix cornélien inutile : je prends une chemise au hasard, et chouette j’ai pris la bonne (étant donné que les chemises sont identiques). Par contre, il faudra pouvoir distinguer les chemises propres et les chemises sales…
-
- 10. Dans un pays où les gens ne veulent que des garçons, les familles continuent d’enfanter jusqu’à ce qu’elles aient un garçon. Si elles ont une fille, elles ont un autre enfant. Si elles ont un garçon, elles s’arrêtent. Quelle est la proportion de garçons par rapport aux filles dans le pays ?
S’il y a autant de chances d’avoir un garçon ou une fille (c’est-à-dire une probabilité de 50% pour chacun), alors même si un pays qui décide de n’avoir que des garçons en pratiquant un natalisme qui engendre des filles jusqu’à avoir des garçons, la proportion reste la même. En effet, que ce soit une natalité naturelle ou alors un natalisme sélectif, il y aura pourtant autant de garçons que de filles.
L’intuition nous induit en erreur en nous laissant croire qu’il y aurait sensiblement plus de garçons que de filles. Empiriquement, la proportion 50%-50% est observée.
La preuve avec ce programme que j’ai écrit en langage Perl :
#!/usr/bin/perl
for ($family = 1; $family <= 1000000; $family++)
{
$a = int(rand(2));
if ($a == 1) { goto label1; }
$b = int(rand(2));
if ($b == 1) { goto label2; }
$c = int(rand(2));
if ($c == 1) { goto label3; }
$d = int(rand(2));
if ($d == 1) { goto label4; }
$e = int(rand(2));
if ($e == 1) { goto label5; }
$f = int(rand(2));
if ($f == 1) { goto label6; }
$g = int(rand(2));
if ($g == 1) { goto label7; }
$h = int(rand(2));
if ($h == 1) { goto label8; }
label1:
print « $a \n »;
goto end;
label2:
print « $a \n »;
print « $b \n »;
goto end;
label3:
print « $a \n »;
print « $b \n »;
print « $c \n »;
goto end;
label4:
print « $a \n »;
print « $b \n »;
print « $c \n »;
print « $d \n »;
goto end;
label5:
print « $a \n »;
print « $b \n »;
print « $c \n »;
print « $d \n »;
print « $e \n »;
goto end;
label6:
print « $a \n »;
print « $b \n »;
print « $c \n »;
print « $d \n »;
print « $e \n »;
print « $f \n »;
goto end;
label7:
print « $a \n »;
print « $b \n »;
print « $c \n »;
print « $d \n »;
print « $e \n »;
print « $f \n »;
print « $g \n »;
goto end;
label8:
print « $a \n »;
print « $b \n »;
print « $c \n »;
print « $d \n »;
print « $e \n »;
print « $f \n »;
print « $g \n »;
print « $h \n »;
goto end;
end:
print « — \n »;
}
———————————————-
Dans un terminal sous Linux, on exécute le programme : ./program.pl >> program.log
Puis on compare la quantité de 0 (filles) par rapport à la quantité de 1 (garçons) :
cat program.log | grep « 0 » | wc -l
cat program.log | grep « 1 » | wc -l
Et je constate des quantités équivalentes.
-
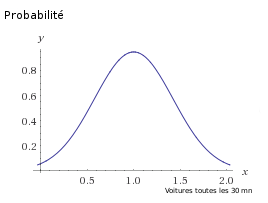
- 11. Si la probabilité d’observer une voiture en 30 minutes sur une route est 0.95, quelle est la probabilité d’observer une voiture en 10 minutes ?
On peut répondre à cette question grâce à la loi de Poisson. Il faudra toutefois calculer d’abord la fréquence moyenne (le nombre moyen de voitures en 30 minutes). Cependant, la probabilité maximum est atteinte lors de la fréquence moyenne des voitures en circulation, et dans le cas de la loi normale gaussienne, l’on sait que la probabilité maximum vaut environ 0,4/s où s est l’écart-type.
C’est-à-dire :  que l’on divise par l’écart-type.
que l’on divise par l’écart-type.
Ainsi, une probabilité de 0,95 suggère que l’écart-type pourrait être faible. Ainsi, si la fréquence du trafic routier de 1 voiture toutes les 30 minutes est la fréquence moyenne, probable à 0,95, cela correspondrait alors à un écart-type de 0,421. Par conséquent, si l’on spécule sur un trafic routier 3 fois plus important (1 voiture toutes les 10 minutes), sa probabilité sera de 0,0000119. Ce qui est nettement plus rare, car l’écart-type est faible, et la probabilité maximale est concentrée autour de la moyenne.
À partir de l’équation de la courbe de Gauss, j’ai pu établir un graphe :
-
- 12. Vous regardez une horloge indiquant 3h15mn, quel est l’angle entre l’aiguille des heures et celle des minutes ? (La réponse n’est pas zéro !)
L’angle est de 7,5°.
-
- 14. Vous êtes à une soirée avec un ami. Dix personnes y sont présentes, dont vous et votre ami. Votre ami parie que si vous trouvez une personne qui est née le même jour que vous, il vous donne 1$; que pour chaque personne qu’il trouve n’étant pas né le même jour que vous, vous lui donnez 2$. Accepteriez-vous le pari ?
Je pose n = 10.
Alors la probabilité P est :
P = 1 – (365!/(365-n)!)(1/365n)
P = 0,1169
La probabilité est de 11,69% de trouver 2 personnes née le même jour, parmi les 10 personnes. Il est donc plus probable de trouver des couples de personnes qui ne sont pas nées le même jour. Le pari est donc risqué.
Toutefois, la probabilité augmente s’il y a plus d’invités. La probabilité atteint 41,14% s’il y a 20 personnes réunies.
Je gagne le pari si la probabilité devenait supérieure à 66,67%, c’est-à-dire en réunissant au moins 28 invités (dont moi et l’ami). Mais avec moins d’invités, la probabilité de perdre est certaine.
C’est intéressant. Comme la théorie des probabilités est beaucoup plus sûre que les pseudo-savoirs intuitifs, vous pouvez créer des paris sur ce principe, et donc de gagner vos paris puisque les calculs de probabilités vous fournissent la bonne solution, tandis que l’intuition est le meilleur moyen de se tromper. 😉
———————————————
- Dans une autre page, d’autres questions attribuées à Google : http://www.presse-citron.net/17-questions-stupides-que-google-ne-pose-plus-en-entretien-de-recrutement/
J’ai tenté de répondre aussi à ces questions.
-
10. Expliquez l’importance de « boeuf mort. »
Réponse de geek : en anglais, « boeuf mort » se dit « dead beef », et cette séquence de lettres correspond à un nombre hexadécimal.
Le nombre hexadécimal deadbeef correspond au nombre décimal 3735928559.
-
11. Si une personne compose d’une séquence de chiffres sur le téléphone, quels mots / chaînes possibles peuvent être formés à partir des lettres associées à ces chiffres ?
Si je compose mon propre numéro de téléphone mobile, je peux composer 6561 combinaisons d’une séquence de 8 lettres, en soulignant que le chiffre 0 et le chiffre 1 ne codent pas pour une lettre donnée, les chiffres 2 et 3 et 4 et 5 et 6 et 8 codent chacun pour 3 lettres, puis les chiffres 7 et 9 codent chacun pour 4 lettres.
Sachant que tous les numéros de téléphones en France commencent par un zéro, je présume qu’on peut composer des « mots » jusqu’à 9 lettres par « mot ». A priori une quarantaine de milliers de mots aléatoires générés par tous les numéros de téléphones possibles. Avec un numéro composé au hasard, il y a des centaines, des milliers ou des dizaines de milliers de combinaisons possibles de lettres.
-
3. A l’aide d’un sablier de 4 minutes et un de 7 minutes, mesurez-en 9 très précisément
Euuuh… J’utilise 4 fois le sablier de 4 minutes (donc 16 minutes en tout), et j’utilise une fois le sablier de 7 minutes afin de « déduire » : 16 – 7 = 9.
Autrement, je ne sais pas. Ou alors j’utilise une fois le sablier de 7 minutes et aussitôt je vide le sablier de 4 minutes jusqu’à sa moitié (2 minutes)…
7. Vous avez une montagne d’argent aussi haute que l’Empire State Building. Pouvez-vous tout mettre dans une pièce ?
Mmmhh… Oui, d’après un certain point de vue. Je fais couler l’argent métallique pour frapper la plus grosse pièce de monnaie du monde. Non ?
–
Bon alors, Google, tu m’embauches ?
–
D’autres questions d’après le lien ci-dessus.
- • Vous êtes dans un couloir de pierre de 2,5 mètres de section. Le Prince des ténèbres apparaît devant vous. Que faites-vous? (question posée chez Microsoft)
Tiens ? ils font de l’humour aussi ? ^^ Que fais-je ? Je donne un violent coup de pied dans les couilles du Prince des Ténèbres. Oui, il en a (enfin il en avait, peu avant), héhé. Parce qu’en Enfer, Satan l’habite (calembour obscène).
- • D’après un sondage, 70% des gens aiment le café, et 80% aiment le thé. Quelles sont les limites supérieures et inférieures pour la proportion de gens qui aiment à la fois le café et le thé?
Je présume que les deux probabilités sont indépendantes entre elles.
Il y a les gens qui aiment le thé et le café, ceux qui aiment l’un ou l’autre, et ceux qui n’aiment ni l’un ni l’autre.
J’ai conçu un petit programme en langage Perl pour distinguer ces différents cas.
#!/usr/bin/perl
for ($i = 1; $i <= 1000000; $i++)
{
$t = int(rand(10));
$c = int(rand(10));
if (($t <= 8) and ($c <= 7))
{
print « TC\n »;
}
if (($t > 8) and ($c > 7))
{
print « 00\n »;
}
if (($t > 8) and ($c <= 7))
{
print « 0C\n »;
}
if (($t <= 8) and ($c > 7))
{
print « T0\n »;
}
}
D’après mon test empirique, je trouve 2% qui n’aiment ni le thé ni le café, et 72% qui aiment à la fois le thé et le café, et 8% qui aiment uniquement le café, et 18% qui aiment uniquement le thé.
- Question par Facebook :
Question de temps « Combien de questions devez-vous poser pour découvrir un nombre entre 1 et 1000, sachant qu’on ne peut vous répondre que par ‘plus haut’ ou ‘plus bas’? »
La question peut paraître bizarre, mais les statistiques peuvent permettre de répondre à cette question avec une marge d’incertitude.
On peut écrire un programme qui indique un nombre au hasard en 1 et 1000, puis selon « plus grand » ou « plus petit », l’intervalle rétrécit et le programme répond toujours aléatoirement à chaque étape de nouvel intervalle. Ainsi, il est possible de quantifier le nombre moyen de questions à poser, et avec une marge.
J’ai réussi à écrire un programme qui devine lui-même le nombre-mystère (entre 1 et 1000).
#!/usr/bin/perl
$i = 0;
$mystery = 1 + int(rand(1000));
$redefini = $mystery;
for ($test = 1; $test <= 100000; $test++)
{
$i++;
$devine = 1 + int(rand($redefini));
if ($devine == $mystery)
{
print « BRAVO ! Number found after $i tests\n »;
goto end;
}
if ($$mystery < $devine)
{
$redefini = 1 + int(rand($devine));
print « Plus petit\n »;
}
if ($mystery > $devine)
{
$calc = 1000 – $devine;
$redefini = $devine + int(rand($calc));
print « Plus grand\n »;
}
}
end:
BILAN : sur 20 tests de réussite, il faut poser 1096 questions en moyenne, plus ou moins un écart-type de 1000.
Sur ces 20 tests, souvent il fallait des centaines de questions, mais parfois il n’en fallait que 19, mais aussi parfois plus de 2300. Ainsi, le nombre de questions à poser est très variable. Mais en moyenne, il faut poser autant de questions qu’il y a de nombres de 1 à 1000. Voila.
-
«Vous êtes dans une pièce sombre, sans lumière. Vous avez besoin de chaussettes assorties pour votre entretien d’embauche et vous avez 19 chaussettes grises et 25 chaussettes noires. Quelles sont vos chances d’avoir une paire assortie?»
Quand je prends 2 chaussettes au hasard, sans en voir leurs couleurs, j’ai (52,1 plus ou moins 3,6) % de chances d’avoir une paire assortie (2 chaussettes grises ou 2 chaussettes noires), d’après un programme empirique. C’est-à-dire légèrement un peu plus d’une chance sur deux.
—
© 2014 john Philip C. Manson

Vous devez être connecté pour poster un commentaire.